「割合」のもととなる数字って?
先日、ダッシュボードの見方のサンプルとして取り上げた福岡県内市区町村の人口データを使った人口ピラミッド(ここでは2024年4月1日現在を例にします)をよくよく見返していたところ、「割合」の考え方にちょっと疑問が出てきました。
この人口ピラミッドでは、人口規模の大小の差が大きい市区町村を並べて表示した際に見比べやすいように、人口の実数とは別に「割合」で比較するグラフも作っていました。
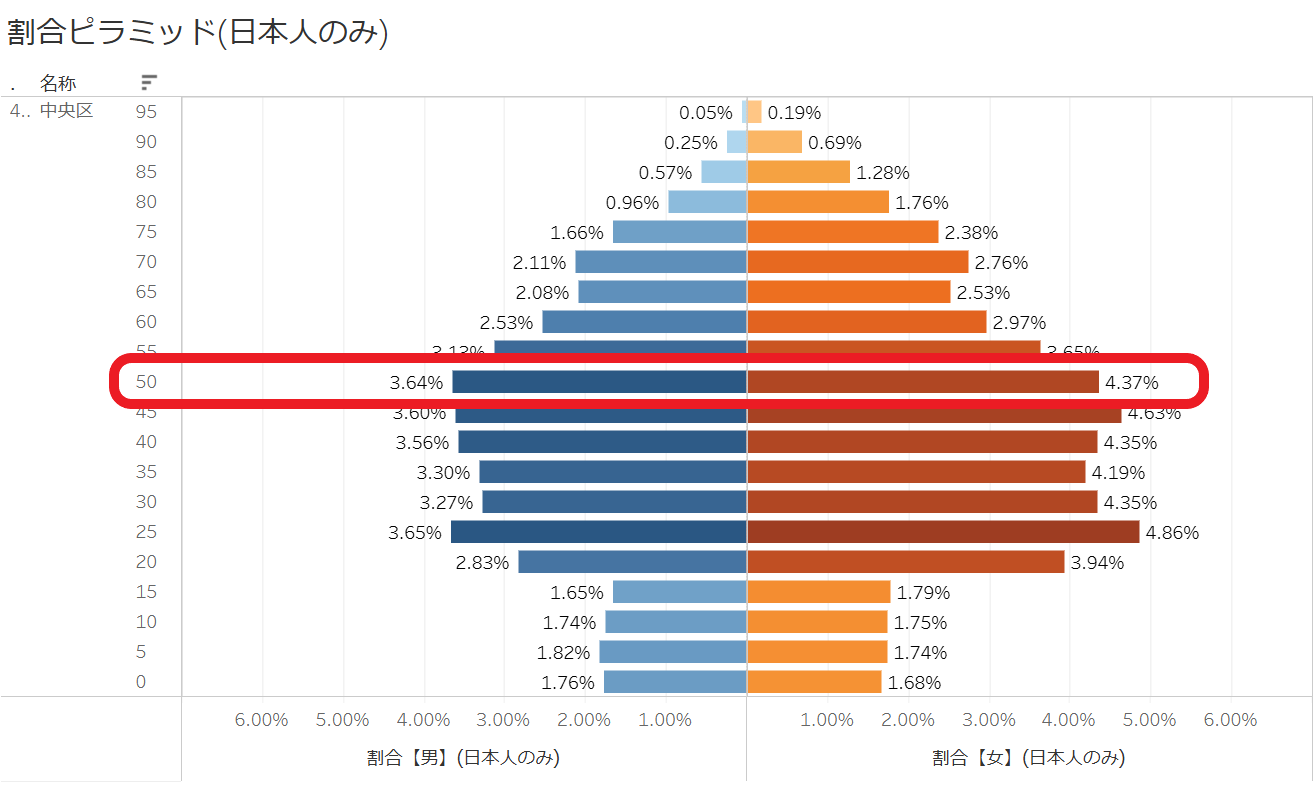
例として、福岡市中央区の割合で表現した人口ピラミッドを見てみましょう。
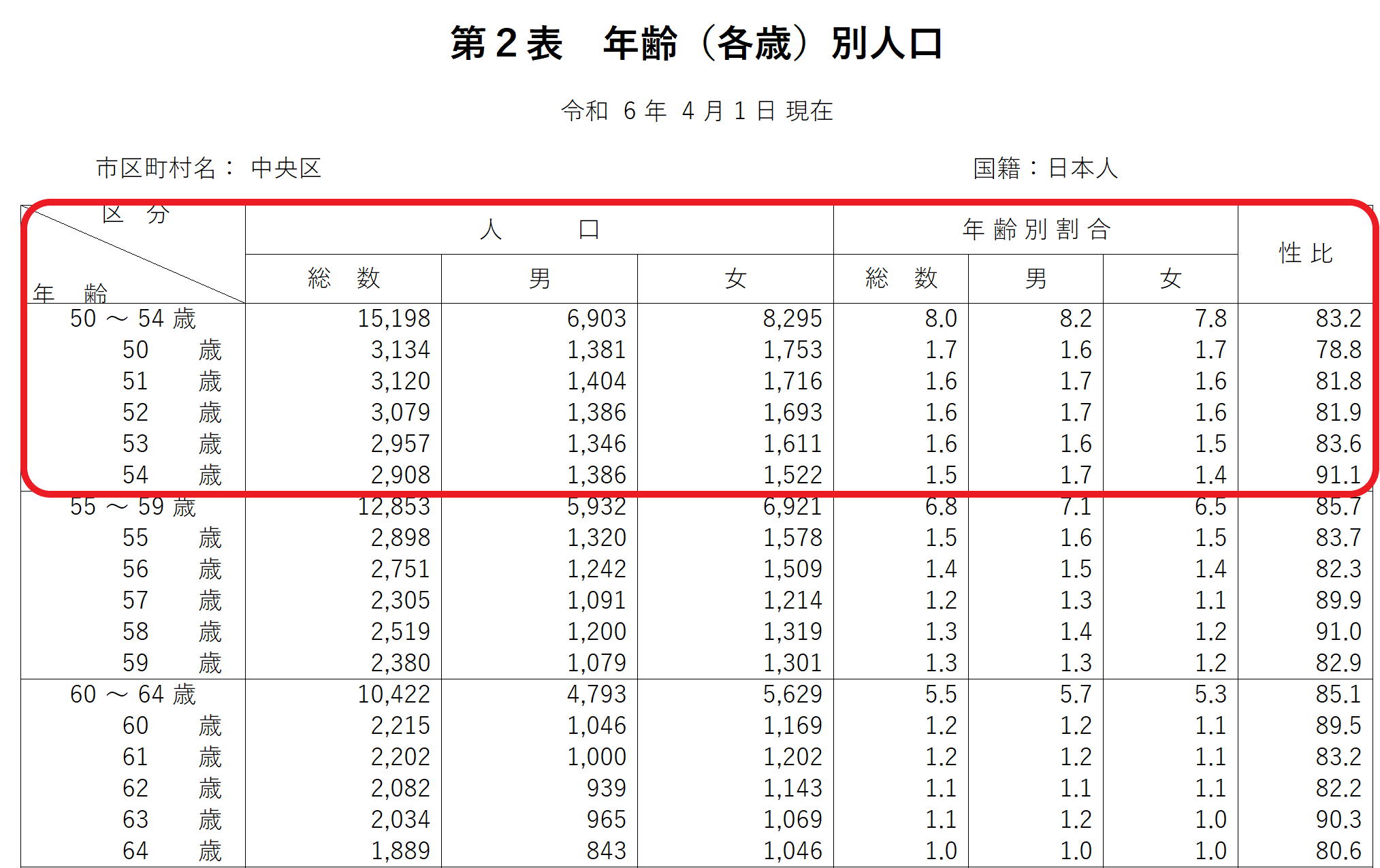
こちらの50-54歳の行を見てみると、男性が8.3%で、女性が7.8%となっています。
はて、以前何かの資料でこのあたりの人口比を確認したときに、福岡市は女性の方が多いという会話をした記憶が……。
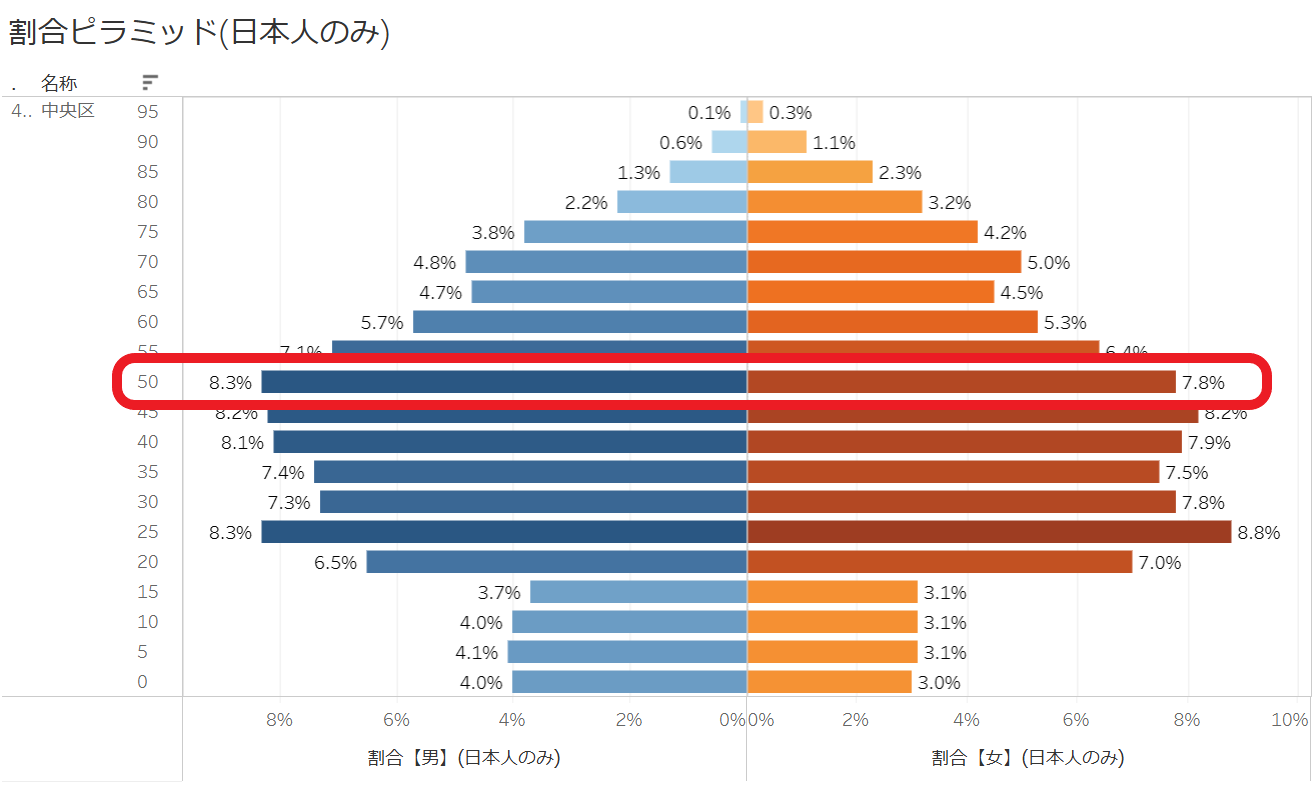
今度は同じ福岡市中央区で、人口の実数で表現した人口ピラミッドを見てみましょう。
こちらの50-54歳の行を見てみると、男性が6,903人で、女性が8,295人。
やはり女性の方が約1,400人多く、「男性が8.3%で、女性が7.8%」という割合となるのは変な気がします。
データソースとした福岡県のオープンデータのExcelにはこの「割合」という数値は直接記録されており、私がグラフを作る際に計算フィールドで算出したものではありません。
※Excel上の50~54歳の「8.2%」ではなく、「8.3%」となっているのは、Tableauの「ビン」という機能で50歳・51歳・52歳・53歳・54歳の数値を合計しているからです。
男女ごと計に対する割合ではなく、市区町村合計に対する割合にしたい!
この福岡市中央区の50-54歳における「男性が8.2%で、女性が7.8%」という割合を逆算してみると、どうやら「各市区町村の、各性別における小計との割合」のようです。
「福岡市中央区の、50-54歳の男性の合計」 = 6,903人 (a)
「福岡市中央区の、「不詳」を除く男性の合計」 = 83,785人 (b)
(a)/(b) = 0.08238945 ≒ 8.2%
「福岡市中央区の、50-54歳の女性の合計」 = 8,295人 (c)
「福岡市中央区の、「不詳」を除く女性の合計」 = 106,028人 (d)
(c)/(d) = 0.07823405 ≒ 7.8%
このように算出している、すなわち「男女それぞれの合計に対する割合」ということは分かりましたが、人口ピラミッドのように男女の対比もしたい場合には、「男女を区別しない合計に対する割合」の方が直感的になると思います。
LOD計算で対処しました
しかし、元のExcelで「男女を区別しない合計に対する割合」を計算してもう一度Tableauに読み込ませるのはあまりスマートな手法ではありません。
こういうときはまず「簡易表計算」で割合をTableau上で計算したいところですが……
今回は詳しい解説は省略しますが、「市区町村」によるディメンションと「性別」によるディメンションが存在しているので、単純に「簡易表計算」を使ってペインや市区町村で区切っての計算ではうまく算出できませんでした。
そこで、まず計算フィールドにて
{FIXED [市区町村]: SUM([人口])}
として、基準を市区町村のディメンションに固定した、市区町村ごとの男女を区別しない合計を算出します。
次に、その計算した値(市区町村ごと人口総数)について
[人口【男】]/[市区町村ごと人口総数]
[人口【女】]/[市区町村ごと人口総数]
という計算フィールドを作成して、分子は男女それぞれの人口、分母は「男女を区別しない合計」として割合を算出しました。
「福岡市中央区の、50-54歳の男性の合計」 = 6,903人 (e)
「福岡市中央区の、「不詳」を除く合計」 = 189,813人 (f)
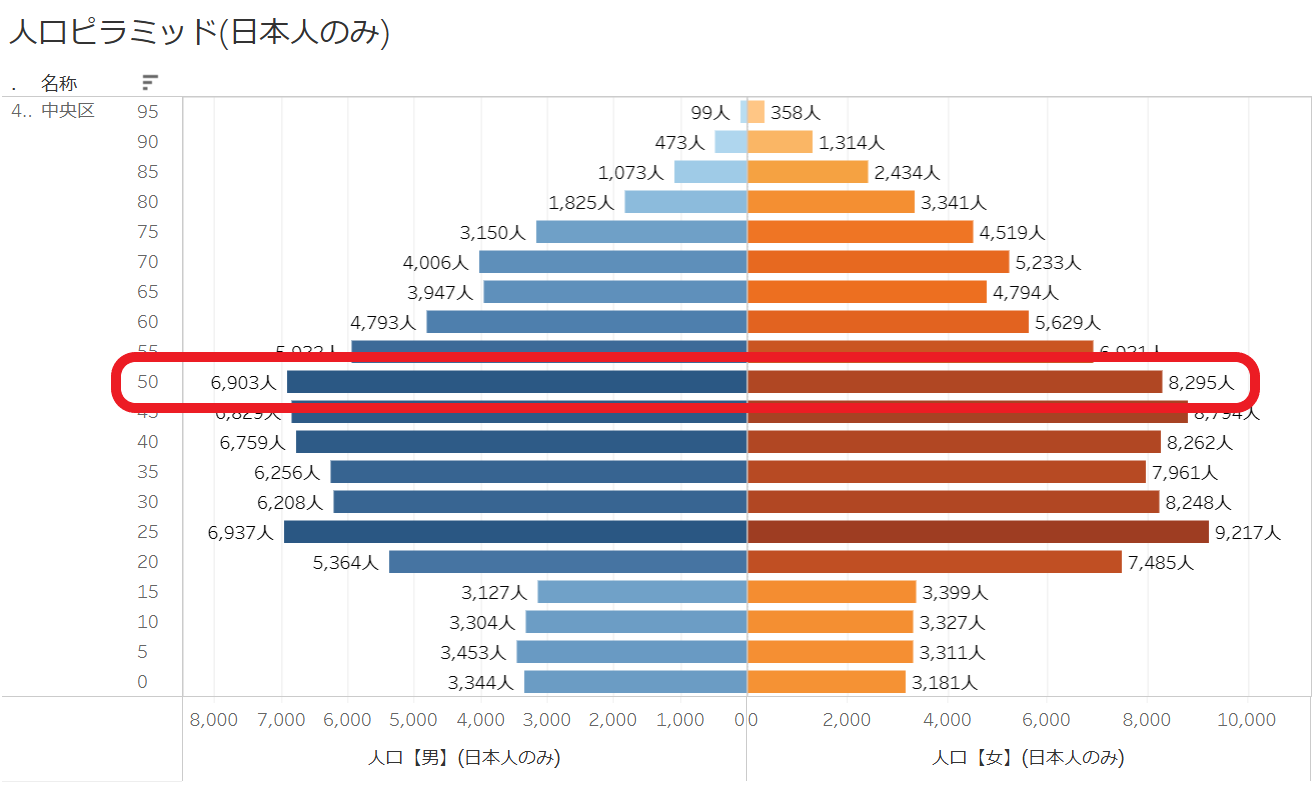
(e)/(f) = 0.03636737 ≒ 3.64%
「福岡市中央区の、50-54歳の女性の合計」 = 8,295人 (g)
「福岡市中央区の、「不詳」を除く合計」 = 189,813人 (f)
(g)/(f) = 0.04370091 ≒ 4.37%
これにより、人口の実数と同じ比率の棒の長さを表現しつつ、人口規模の大小の差が大きい市区町村を並べても、小規模市町村の棒が短くなりすぎない表現ができました。
コメント